Redes Neurais Recorrentes#
As redes neurais recorrentes (RNNs) foram desenvolvidas para lidar com dados sequenciais, como séries temporais, sinais ou texto, onde a ordem das entradas carrega significado. Diferentemente das MLPs e CNNs, que tratam as entradas de forma independente, as RNNs introduzem conexões recorrentes que permitem manter um estado interno (memória), propagando informações de passos anteriores para os seguintes. Essa característica possibilita modelar dependências temporais de curto prazo, tornando-as adequadas para tarefas como reconhecimento de fala, tradução automática e previsão de séries temporais.
A estrutura básica de uma RNN consiste em uma célula recorrente que recebe a entrada atual e o estado oculto anterior, gerando uma nova representação que será usada tanto para a saída quanto para o próximo passo temporal. Essa recorrência permite compartilhar parâmetros ao longo da sequência, reduzindo a complexidade do modelo em comparação com arquiteturas totalmente conectadas aplicadas diretamente a sequências. Entretanto, RNNs tradicionais sofrem com problemas de gradientes explosivos e desvanecentes, limitando sua capacidade de capturar dependências de longo prazo. Para mitigar isso, variantes como LSTMs (Long Short-Term Memory) e GRUs (Gated Recurrent Units) foram propostas, introduzindo mecanismos de portas que regulam o fluxo de informações. Assim, as RNNs e suas variantes dominaram o processamento sequencial até a ascensão de arquiteturas baseadas em attention, como os Transformers.

RNNs Clássicas e Backpropagation Throught Time#
As RNNs clássicas processam sequências de dados com base em uma memória interna que se atualiza a cada novo passo da sequência, permitindo que a rede armazene informações sobre entradas anteriores. Isso é possível porque cada neurônio recebe, além da entrada atual, o estado oculto da etapa anterior, o que permite que as redes RNN processem uma sequência de dados etapa por etapa.
O treinamento dessas redes utiliza um algoritmo conhecido como Backpropagation Through Time (BPTT), que é uma extensão do tradicional backpropagation para dados sequenciais (Werbos, 1990). No BPTT, os erros são retropropagados não apenas através das camadas da rede, mas também ao longo do tempo, de uma etapa da sequência para a anterior. Isso permite que a RNN aprenda dependências temporais, ajustando os pesos para minimizar o erro em várias etapas.

No entanto, RNNs simples podem sofrer com problemas de gradiente desvanecente, dificultando o aprendizado de dependências de longo prazo. Para lidar com isso, variantes como LSTM (Long Short-Term Memory) e GRU (Gated Recurrent Unit) foram desenvolvidas, introduzindo mecanismos que controlam o fluxo de informações e preservam a memória por períodos mais longos, tornando-as mais eficazes em capturar padrões complexos em dados sequenciais.
LSTM (1997)#
A LSTM (Long Short-Term Memory) é uma variante avançada das RNNs, projetada para lidar com o problema do gradiente desvanecente, que afeta as redes recorrentes clássicas quando tentam aprender dependências de longo prazo. Introduzida por Hochreiter e Schmidhuber em 1997, a LSTM utiliza um sistema de portas (entrada, esquecimento e saída) que controla o fluxo de informações em cada célula da rede. A porta de esquecimento decide quais informações devem ser descartadas da memória, enquanto a porta de entrada atualiza a memória com novas informações e a porta de saída seleciona o que será passado para a próxima etapa. Esse mecanismo permite que a LSTM preserve e manipule informações ao longo de grandes intervalos de tempo, tornando-a muito eficaz para tarefas que exigem capturar dependências complexas e de longo prazo, como tradução automática, reconhecimento de fala e previsão de séries temporais. A LSTM foi um avanço crucial no campo de redes recorrentes, permitindo um aprendizado mais eficiente e robusto em sequências longas.

GRU (2014)#
A GRU (Gated Recurrent Unit) é uma variante das redes LSTM, proposta por Cho et al. em 2014, que simplifica o design das LSTMs, mantendo muitos de seus benefícios. Diferente da LSTM, a GRU combina as funcionalidades das portas de entrada e de esquecimento em uma única porta de atualização, e usa uma porta de reset para controlar a quantidade de informação que flui do estado anterior para o atual. Essa simplificação torna a GRU mais eficiente em termos de computação e memória, já que ela tem menos parâmetros do que a LSTM, sem sacrificar o desempenho em muitas tarefas. A GRU é particularmente eficaz para capturar dependências temporais de curto e longo prazo, tornando-a uma escolha popular em aplicações como tradução automática, modelagem de séries temporais e reconhecimento de fala. Devido à sua simplicidade e desempenho comparável ao da LSTM, a GRU é frequentemente usada quando há necessidade de redes mais leves e rápidas.

Redes Bidirecionais#
As BiLSTM (Bidirectional Long Short-Term Memory) e BiGRU (Bidirectional Gated Recurrent Unit) são versões bidirecionais das arquiteturas LSTM e GRU, projetadas para capturar informações tanto do passado quanto do futuro em uma sequência de dados. Em vez de processar os dados apenas em uma direção (do início ao fim), essas redes utilizam duas camadas recorrentes: uma que processa a sequência na ordem tradicional e outra que processa na ordem inversa (Schuster et al., 1997). Essa abordagem permite que as redes bidirecionais captem dependências contextuais de ambas as direções, o que é especialmente útil em tarefas como tradução automática, onde o significado de uma palavra pode depender tanto do contexto anterior quanto do posterior, ou em reconhecimento de fala, onde a compreensão de um som pode ser influenciada por fonemas adjacentes. A BiLSTM é mais flexível, devido ao seu controle mais refinado de memória com as três portas, enquanto a BiGRU, por ser mais simples e eficiente, é preferida em cenários onde o desempenho computacional é uma prioridade. Ambas são amplamente usadas em processamento de linguagem natural e tarefas sequenciais complexas.

Seq2Seq#
As arquiteturas Seq2Seq (Sequence-to-Sequence) são redes neurais projetadas para transformar uma sequência de entrada em outra sequência de saída, sendo amplamente utilizadas em tarefas como tradução automática, resumo de texto e reconhecimento de fala (Sutskever et al, 2014). A arquitetura típica envolve um encoder e um decoder, ambos normalmente compostos por redes neurais recorrentes (RNNs), como LSTMs ou GRUs, ou versões mais recentes com Transformers. O encoder processa a sequência de entrada e gera uma representação vetorial (um estado oculto), que captura as informações relevantes da entrada. O decoder, por sua vez, utiliza essa representação para gerar a sequência de saída, um elemento por vez. A transição entre o encoder e o decoder pode ser facilitada por um mecanismo de atenção, que permite que o decoder se concentre em diferentes partes da entrada enquanto gera cada elemento da saída, melhorando a precisão em tarefas complexas, como tradução.

Normalização em Redes Neurais Recorrentes#
Redes Neurais Recorrentes podem lidar com sequências de comprimento variável, como frases ou parágrafos, onde cada token depende de sua posição na sequência. O BatchNorm, que normaliza as ativações com base em todo o lote, pode interferir nessas dependências temporais.
Layer Normalization#
Por outro lado, a Layer Normalization (LayerNorm) normaliza cada amostra de forma independente, sem depender de outras amostras no lote, preservando assim as dependências temporais e contextuais dentro das sequências. A LayerNorm foi introduzida em 2016, por Jimmy Lei Ba, Jamie Ryan Kiros e Geoffrey Hinton. A técnica foi desenvolvida para normalizar as ativações das camadas de redes neurais recorrentes de forma independente em cada amostra, ao invés de calcular as estatísticas em lotes de dados como no Batch Normalization.

Exemplo de Séries Temporais#
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from tqdm import tqdm
from torch.utils.data import Dataset, DataLoader
df = pd.read_csv('https://raw.githubusercontent.com/vhrique/anne_ptbr/refs/heads/main/data/box-jenkins-gas-furnace.txt')
df_train = df.iloc[:-100]
df_test = df.iloc[-100:]
df_mean = df_train.mean()
df_std = df_train.std()
df_train_norm = (df_train - df_mean) / df_std
df_test_norm = (df_test - df_mean) / df_std
class TimeSeriesDataset(Dataset):
def __init__(self, dataframe, sequence_length=10):
self.data = dataframe.values
self.sequence_length = sequence_length
def __len__(self):
return len(self.data) - self.sequence_length
def __getitem__(self, idx):
x = self.data[idx:idx+self.sequence_length, :]
y = self.data[idx+self.sequence_length, :]
return torch.tensor(x, dtype=torch.float32), torch.tensor(y, dtype=torch.float32)
sequence_length = 10
train_dataset = TimeSeriesDataset(df_train, sequence_length)
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
test_dataset = TimeSeriesDataset(df_test, sequence_length)
test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)
def train_model(model, dataloader, criterion, optimizer, num_epochs=10, device="cpu"):
model.train() # Set the model to training mode
losses = []
for epoch in tqdm(range(num_epochs)):
running_loss = 0.0
# tqdm no loop de batches
for batch_x, batch_y in dataloader:
batch_x, batch_y = batch_x.to(device), batch_y.to(device)
# Zero the parameter gradients
optimizer.zero_grad()
# Forward pass
outputs = model(batch_x)
# Compute the loss
loss = criterion(outputs, batch_y)
# Backward pass and optimization
loss.backward()
optimizer.step()
# Accumulate the loss
running_loss += loss.item() * batch_x.size(0)
epoch_loss = running_loss / len(dataloader.dataset)
losses.append(epoch_loss)
print('Finished Training')
# Plot das perdas
plt.figure(figsize=(6,4))
plt.plot(range(1, num_epochs+1), losses, marker='o')
plt.title("Training Loss")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.grid(True)
plt.show()
def evaluate_model(model, dataloader, criterion):
model.eval() # Set the model to evaluation mode
eval_loss = 0.0
all_outputs = []
all_labels = []
with torch.no_grad(): # Disable gradient computation during evaluation
for batch_x, batch_y in dataloader:
# Forward pass
outputs = model(batch_x)
# Compute the loss
loss = criterion(outputs, batch_y)
# Accumulate the loss
eval_loss += loss.item() * batch_x.size(0)
all_outputs.extend(outputs.detach().tolist())
all_labels.extend(batch_y.tolist())
avg_loss = eval_loss / len(dataloader.dataset)
print(f'Evaluation Loss: {avg_loss:.4f}')
all_outputs = np.array(all_outputs)
all_labels = np.array(all_labels)
return all_outputs, all_labels
class TimeSeriesMLP(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(TimeSeriesMLP, self).__init__()
self.flatten = nn.Flatten()
self.fc1 = nn.Linear(input_size, hidden_size)
self.relu = nn.ReLU()
self.fc2 = nn.Linear(hidden_size, output_size)
def forward(self, x):
x = self.flatten(x)
x = self.fc1(x)
x = self.relu(x)
x = self.fc2(x)
return x
num_features = df_train.shape[1]
input_size = sequence_length * num_features
hidden_size = 64
output_size = num_features
model = TimeSeriesMLP(input_size=input_size, hidden_size=hidden_size, output_size=output_size)
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
num_epochs = 200
train_model(model, train_loader, criterion, optimizer, num_epochs)
all_outputs, all_labels = evaluate_model(model, test_loader, criterion)
100%|██████████| 200/200 [00:02<00:00, 70.95it/s]
Finished Training
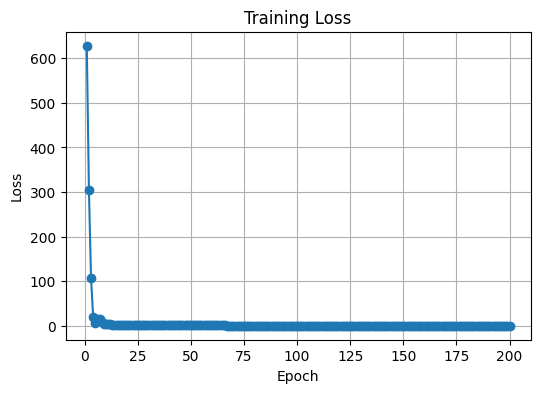
Evaluation Loss: 0.8090
outputs = all_outputs * df_std.to_numpy() + df_mean.to_numpy()
labels = all_labels * df_std.to_numpy() + df_mean.to_numpy()
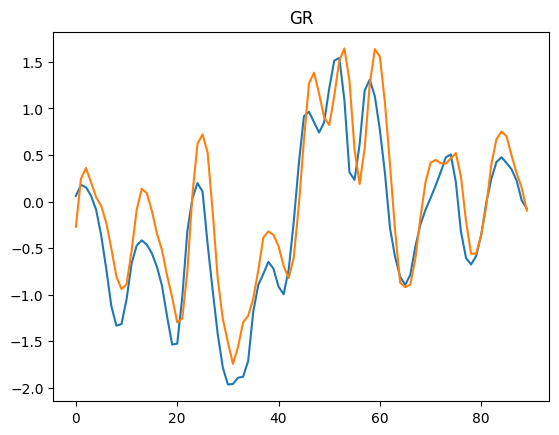
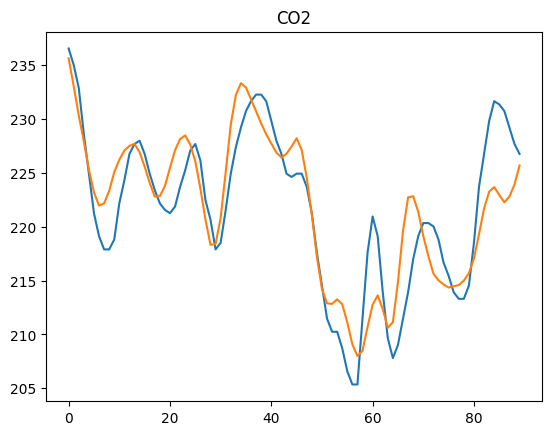
for i in range(2):
plt.plot(labels[:,i])
plt.plot(outputs[:,i])
plt.title(df_std.index[i])
plt.show()
class TimeSeriesLSTM(nn.Module):
def __init__(self, input_size, hidden_size, output_size, num_layers=1):
super(TimeSeriesLSTM, self).__init__()
self.hidden_size = hidden_size
self.num_layers = num_layers
self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True)
self.fc = nn.Linear(hidden_size, output_size)
def forward(self, x):
# Initialize hidden state and cell state (h0, c0)
h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(x.device)
c0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(x.device)
# Forward propagate through LSTM
out, _ = self.lstm(x, (h0, c0))
# Take only the last output for the fully connected layer
out = self.fc(out[:, -1, :])
return out
hidden_size = 64
output_size = num_features
num_layers = 1
model = TimeSeriesLSTM(input_size=num_features, hidden_size=hidden_size, output_size=output_size, num_layers=num_layers)
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
num_epochs = 200
train_model(model, train_loader, criterion, optimizer, num_epochs)
all_outputs, all_labels = evaluate_model(model, test_loader, criterion)
100%|██████████| 200/200 [00:08<00:00, 24.95it/s]
Finished Training
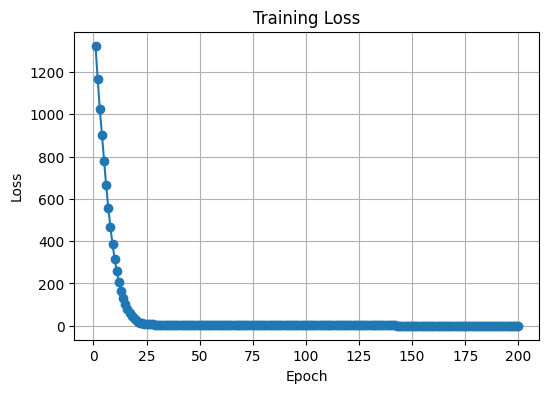
Evaluation Loss: 0.5830
outputs = all_outputs * df_std.to_numpy() + df_mean.to_numpy()
labels = all_labels * df_std.to_numpy() + df_mean.to_numpy()
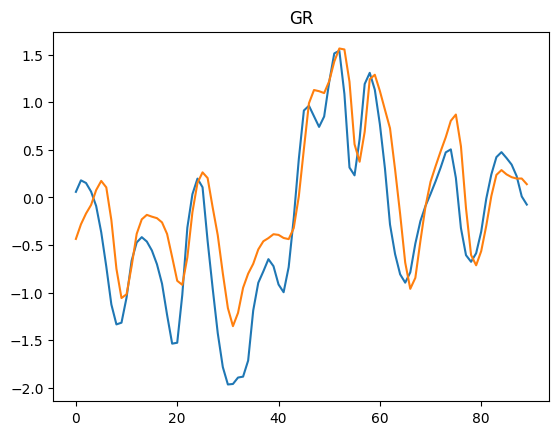
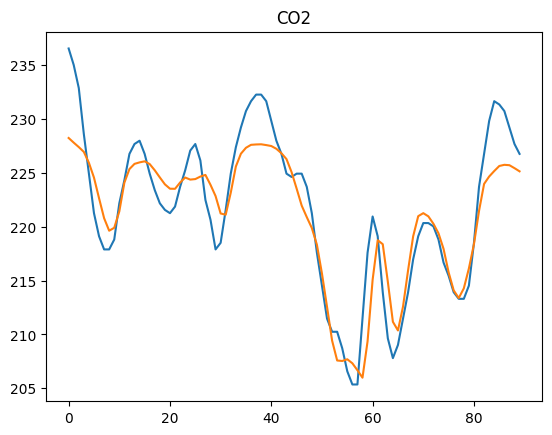
for i in range(2):
plt.plot(labels[:,i])
plt.plot(outputs[:,i])
plt.title(df_std.index[i])
plt.show()
Considerações Finais#
Neste capítulo, abordamos arquiteturas fundamentais de redes neurais para processamento de sequencias, as RNNs, projetadas para lidar com dados sequenciais, como séries temporais e texto, capturando dependências temporais
Desafios de Redes Neurais Recorrentes#
As RNNs apresentam desafios importantes, principalmente quando se trata de capturar dependências de longo prazo em dados sequenciais. Devido ao problema do gradiente desvanecente, as RNNs tendem a perder informações importantes conforme as dependências se tornam mais distantes ao longo da sequência, resultando em um aprendizado menos eficaz. Além disso, o processamento sequencial, onde cada etapa depende da anterior, torna o treinamento computacionalmente caro e difícil de paralelizar, limitando a eficiência da rede em grandes volumes de dados. Essas limitações prejudicaram o desempenho das RNNs em tarefas que requerem a análise de contextos mais longos e levaram à busca por soluções mais avançadas.
Próximo Capítulo#
No próximo capítulo, abordaremos uma arquitetura mais recente, conhecida como transformers, que é capaz de tratar dados sequencias ou espaciais.
Exercícios#
Porque a LSTM foi mais eficiente que a MLP?
Altere a LSTM por uma GRU no exemplo. Qual foi o resultado?
Referências#
Werbos, P. J. (1990). Backpropagation through time: what it does and how to do it. Proceedings of the IEEE, 78(10), 1550-1560.
Hochreiter, S. (1997). Long Short-term Memory. Neural Computation MIT-Press.
Cho, K. (2014). On the Properties of Neural Machine Translation: Encoder-decoder Approaches. arXiv preprint arXiv:1409.1259.
Schuster, M., & Paliwal, K. K. (1997). Bidirectional recurrent neural networks. IEEE transactions on Signal Processing, 45(11), 2673-2681.
Sutskever, I., Vinyals, O., & Le, Q. V. (2014). Sequence to sequence learning with neural networks. Advances in neural information processing systems, 27.
Ba, J. L. (2016). Layer normalization. arXiv preprint arXiv:1607.06450.